Exercise 7.2#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
\(\hat{g} = arg\) \(min_g(\sum_{i=1}^{n} (y_i - g(x_i))^2 + \lambda \int(g^{(m)}(x))^2 dx)\)
\(arg\) \(min_g\) is the value of g that minimizes the function.
(a)#
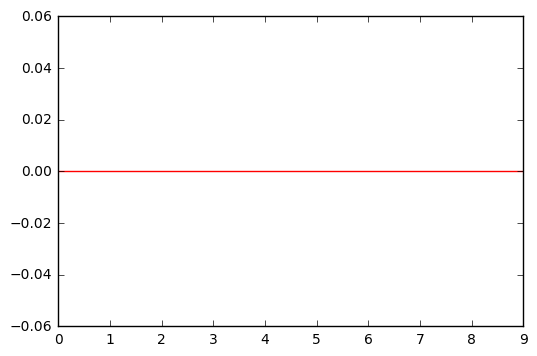
When \(\lambda = \infty\) the first term loses significance and can be ignored. If \(g^{(0)}(x) = g(x) = 0\) the function will be minimized, which means that \(\hat{g}\) must be 0.
# Example sketch
x = np.arange(0,10,1)
y = np.full(10,0,dtype='int')
plt.plot(x,y,'-r');
(b)#
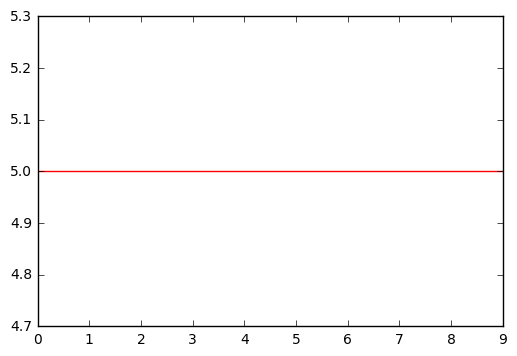
When \(\lambda = \infty\) the first term loses significance and can be ignored. If \(g^{(1)}(x) = g'(x) = c\) the function will be minimized because the first derivative of a constant is 0. This means that \(\hat{g}\) must be an horizontal line.
# Example sketch
# We used c=5 but it could have been done with any other c.
x = np.arange(0,10,1)
y = np.full(10,5,dtype='int')
plt.plot(x,y,'-r');
(c)#
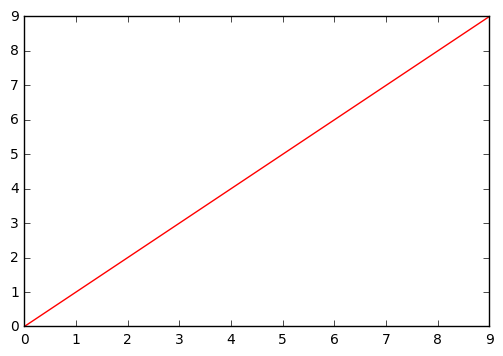
When \(\lambda = \infty\) the first term loses significance and can be ignored. If \(g^{(2)}(x) = g''(x) = bx + c\) the function will be minimized because the second derivative of a linear function is 0. This means that \(\hat{g}\) must be a linear function.
# Example sketch
# We used y=x but it could have been done with any other linear function.
x = np.arange(0,10,1)
y = np.arange(0,10,1)
plt.plot(x,y,'-r');
(d)#
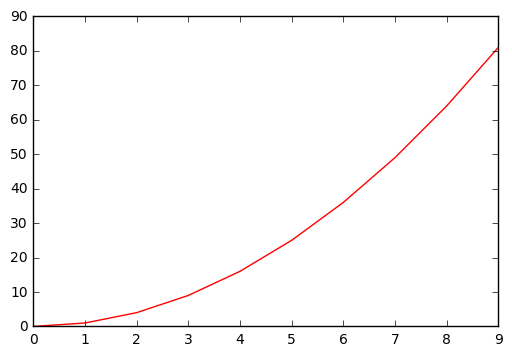
When \(\lambda = \infty\) the first term loses significance and can be ignored. If \(g^{(3)}(x) = g'''(x) = ax^2 + bx + c\) the function will be minimized because the third derivative of a quadratic function is 0. This means that \(\hat{g}\) must be a quadratic function.
# Example sketch
# We used y=x^2 but it could have been done with any other quadratic function.
x = np.arange(0,10,1)
y = np.arange(0,10,1)**2
plt.plot(x,y,'-r');
(e)#
This situation corresponds to a linear regression least squares fit. If \(\lambda = 0\), the second term loses significance and can be ignored. Therefore, the function will be minimized when \(\sum_{i=1}^{n} (y_i - g(x_i)^2\) is minimum. This means that \(\hat{g}\) must be such that it interpolates all of the \(y_i\).
Since there are many different shapes that can express this situation, we didn’t draw any example sketch.
